Category: Case Study

Graph Theory in Roblox (Part 3 – A Solution)

In the previous article, I described a problem I faced when developing a game with little dudes roaming around a pre-built map. In this article, I’ll outline how I applied graph theory (described in the first article) to solve my problem.

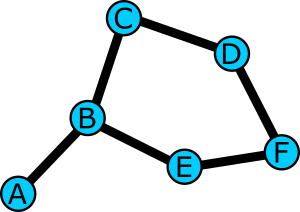
Graphs are about relationships between objects. On my map, there are places that I know a minion can be, and I know which of those places can be accessed from nearby places. I placed parts in Roblox Studio on my map to quickly identify such locations:

Locations on the map that are navigable. Pink nodes represent a path; yellow represents a junction.

Inside each of these Parts, I added ObjectValues whose Values point to adjacent locations in which a minion should be able to travel between. This is essentially building an adjacency list, where each node contains a list of adjacent nodes. This is one of the two main ways to represent a graph in memory; the other method is to store an adjacency matrix of size n-by-n, where n is the number of nodes in a graph. However, I am working with a sparse graph, which means the 100+ nodes only connect to a select few (2-6) other nodes near to them.

Now I have a representation of my map’s network of navigable areas. At runtime, I have the game convert my Parts and ObjectValues into nodes and edges in a graph. The weights of the edges are the euclidean distance between the nodes. If you’d like to view my implementation of graph, node and edge objects, you can download an rbxmx file here. If you’d like to view the source code of each script individually, here are some pastebin links:

The algorithm I selected for shortest path calculation  is the Floyd-Warshall algorithm. For my fellow CS nerds, it runs in order n-cubed time (for every n nodes, we perform n×n×n steps). This algorithm finds all possible paths between all nodes and leaves each node a list of nodes one should travel to if they are to reach a specific destination node. In other words, imagine an n-by-n table, on the left is your current node, on the top is your destination node. It fills out the table with an adjacent node one ought to which one should travel.

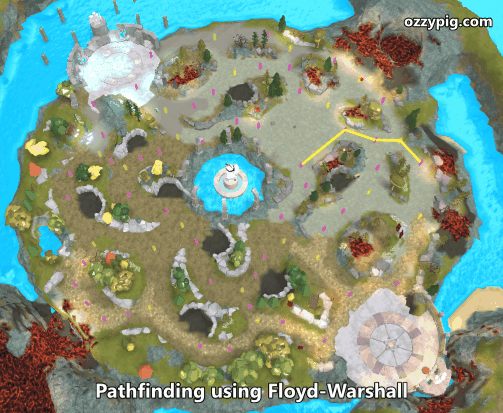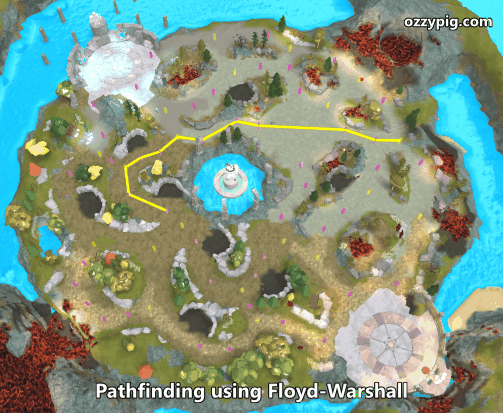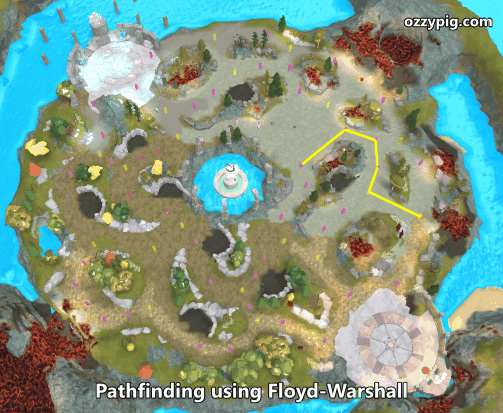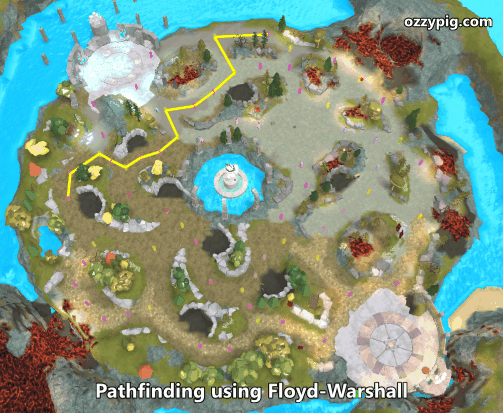
Using the results of the Floyd-Warshall algorithm to find the shortest path between two nodes on a graph.

Above is an animation of randomly chosen paths being rendered in sequence. Here is my implementation (also included in the rbxmx file above) as a mix-in for the Graph class:

The result is pretty awesome! Now, all I do is spawn minions at a random node and randomly choose another random node to path towards. And finally here’s a preview of the two minions using the generated paths.

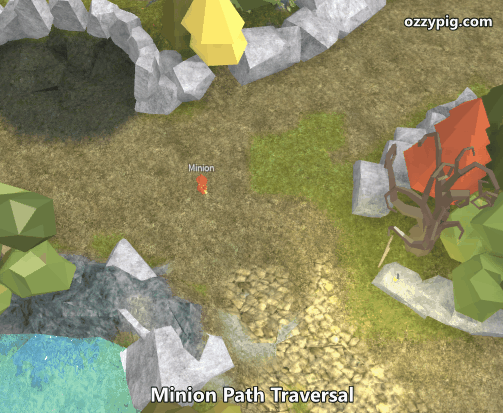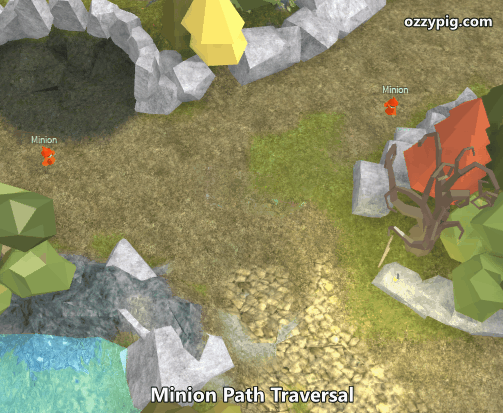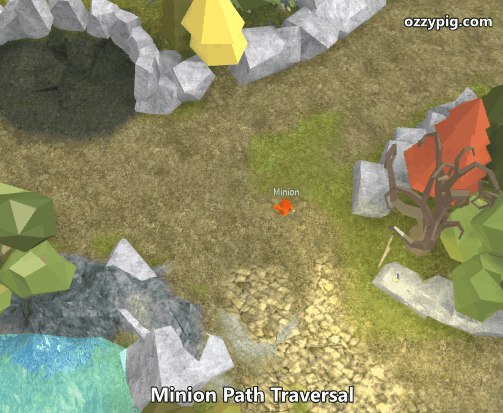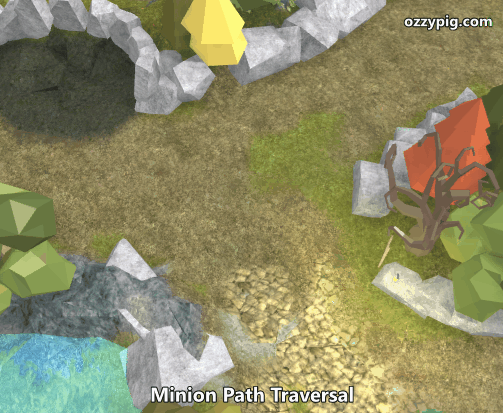
Two minions traversing different paths.

Got questions or comments? Drop me a direct message on Twitter or a message on Roblox.com! I’d love to update this article series with more information.

Graph Theory in Roblox (Part 2 – A Problem)

In the previous article, I went over basic graph theory terms and concepts. Click here to read that article. In this one, I’m going to describe a game design problem I found while working on my project.

First, some background information on my project. Without going into too much detail, it involves two teams roaming a map killing neutral monsters as an objective. One of these neutral monsters I’m calling creeps or minions, similar to those in Defense of the Ancients 2 and League of Legends. In those games, minions align with a team and march  down set paths and assault enemy structures on those paths. However, in my game, minions aren’t on a team, don’t attack structures, and have no set path. Here’s an early draft of the map I’m using:

An early draft of the map (not final). Notice the navigable paths through the map. Click to view the full image.

Minions roam this map freely, and one challenge I’m facing is programming the minion roaming behavior.  I came up with a number of ideas immediately. Here’s some of them:

  • Just walk in some random navigable direction, changing direction if they run into a wall
  • Create a bunch of paths and pick one to follow
  • Pick a random target on the map and use Roblox’s pathfinding to do the hard work for me in finding a path to the point

Well, there’s going to be a lot of minions around this map. Maybe they’ll even travel in packs, who knows! I can’t have the minions raycasting for walls, and I can’t use expensive pathfinding for them to navigate. I also don’t want them switching directions a lot; I’d rather they travel a long path instead of small segments.

How did I apply graph theory to this problem? Find out in the next article.

Graph Theory in Roblox (Part 1 – Intro)

Hey, everyone. Some of you might not know this, but I’m a big nerd when it comes to the topic of computer science. Coding, functions, runtime analysis, space complexity, algorithms… you name a CS topic, I’m probably interested in it. In this series of articles I’m going to outline how I used graph theory, a fundamental topic of computer science, in developing a feature for my current project.

In this article series, I want to give a surface-level introduction to graph theory and showcase the solution to a problem from one of my projects

First and foremost, let’s talk about what graph theory is by defining some of the terms. A graph is a set of vertices (aka nodes), which have edges (aka arcs) connecting them. Two vertices are adjacent if they share an edge. An undirected graph is one in which edges have no direction (edges are lines), and the edges in a directed graph have a direction (edges are arrows). A weighted graph assigns a value to edges

A graph of nodes A through F. Edges: AB, BC, CD, DF, BE, DF
A basic graph with 6 nodes and 6 edges.

Pictured above is a representation of an unweighted, undirected graph featuring nodes labelled A through F. This graph could represent many real-world ideas:

  • A physical map of cities connected by highways
  • A social network of people connected by friendships
  • A set of game board states connected by moves you have to make to get from one state to another
  • A final boss’ attack pattern (nodes are unique attack states, edges are transitions)

Notice how not all of these examples are physical things! They are instead collections of things and relationships between those things. I hope you can start to imagine the many different applications of graphs to real-world problems. Many algorithms have been dreamed up to solve problems involving graphs. To name just a few:

  • Breadth-first (BFS) and depth-first search (DFS) – Two methods of visiting all the nodes in a graph but in different orders
  • Dijkstra’s algorithm – For weighted graphs, find the lowest cost path between two nodes (you cannot use negative edge weights).
  • The Bellman-Ford algorithm – Similar to Dijkstra’s and slower, except you can use negative edge weights (however, there must not be any negative cycles in the graph – a cycle of edges that sum to a negative number)
  • The Floyd-Warshall algorithm – For weighted graphs, calculate all of the paths from each node to every other node.
  • Prim’s algorithm – For weighted graphs, find a minimum spanning tree that visits all nodes, and picks edges so that all nodes are part of the complete graph, while also minimizing costs of used edges.

In the next article, I’ll describe a problem that I identified while working on my project. Later, I show how one of these solve my problem. Click here for part 2 of this series.